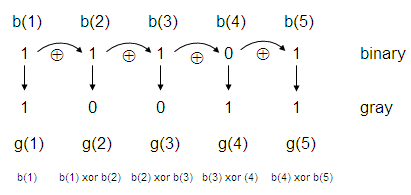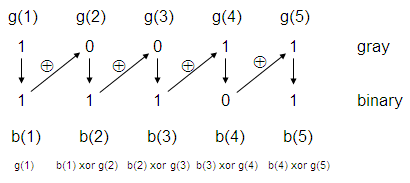九連環遊戲與解法 (Nine Linked Rings Game & Solution)

緣起

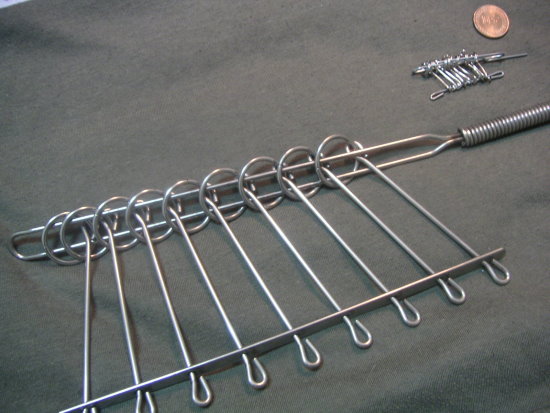
讀國中時吧！某天，大哥帶回一個純手工打造的九連環，當時只看著大哥玩得不亦樂乎，但並沒有引起我太大的興趣；直到大學時再次接觸，才發現原來九連環是有遞迴性的，那時就想寫個程式來解它，記得已動手寫程式了，但應該是當天有事外出吧，回來後就把這件事給忘了。 2007年到宜蘭國立傳統藝術中心時又發現它，這次總算把遞迴程式完成了，當時叫小孩來看九連環的動作，看看後就跑去玩他的玩具了，當時的他應該看不懂吧！

各種連環


純手工打造(參1)	標準形(參2)

直立式(參3)	四連環(參4)

玉女穿梭	扭出來(Spin Out) (參5)

九連環的玩法

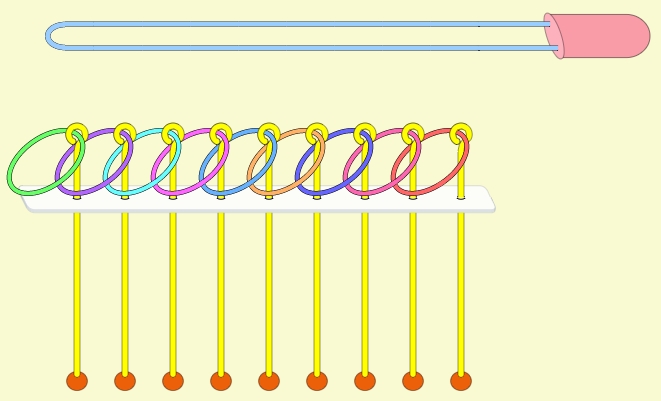
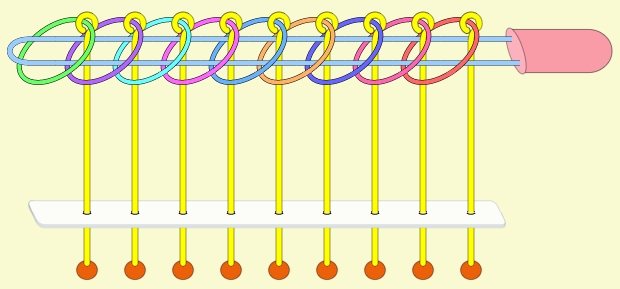
        九連環由九個相互連接的環及一個中空的長形柄所組成。
        九連環的一般玩法有兩種，第一種是將這九個環從柄上取下來，第二種是反過來將九個環放入長柄中。
        另外也可以由任意狀態解成九個環全取下或全放上的玩法。

九個相互連接的環及中空的長形柄

九個環全放入長柄的狀態

九個環的任意狀態

九連環的規則

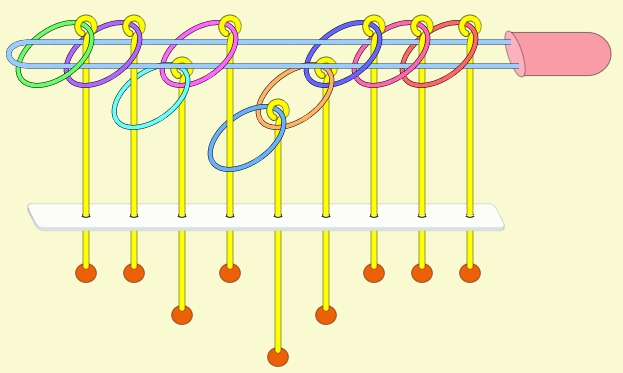
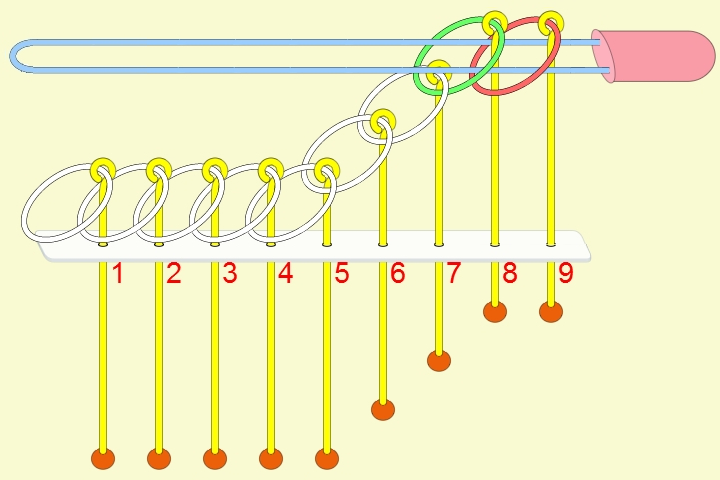
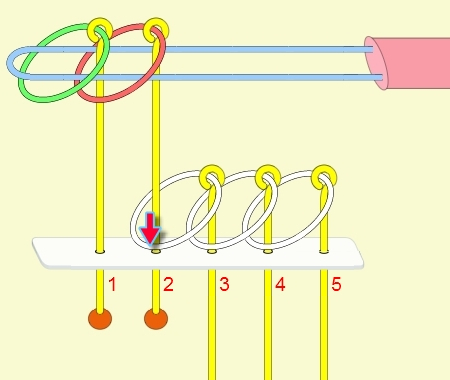
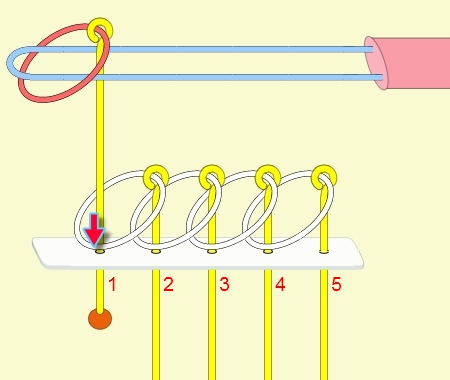
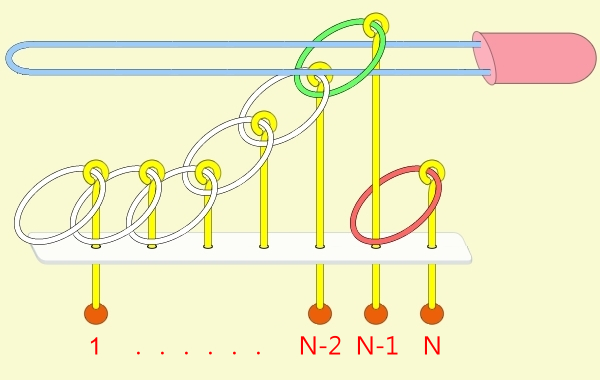
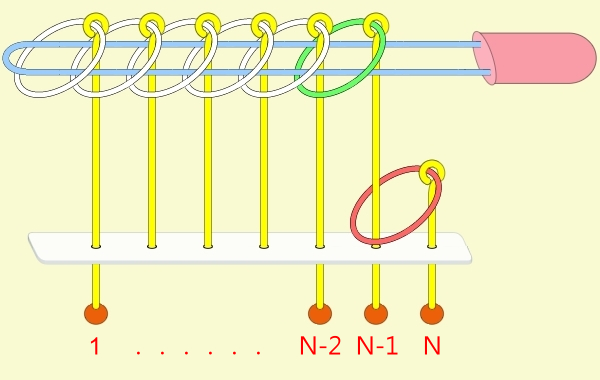
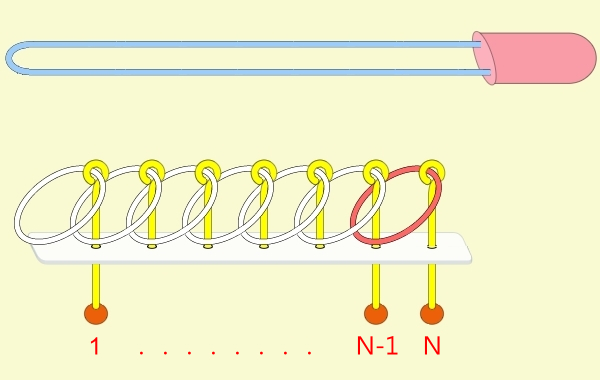
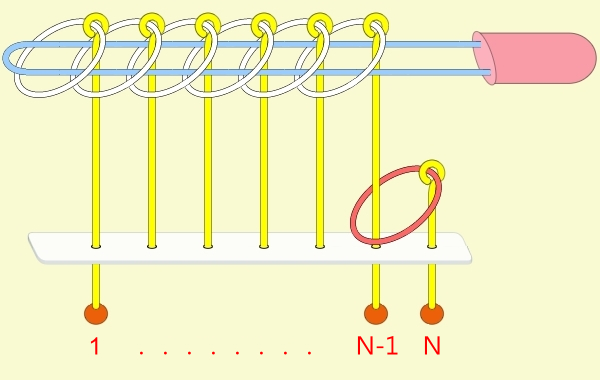
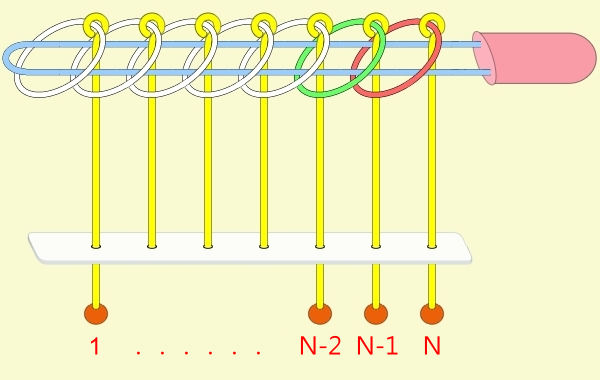
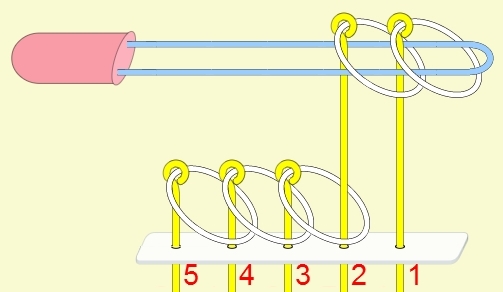
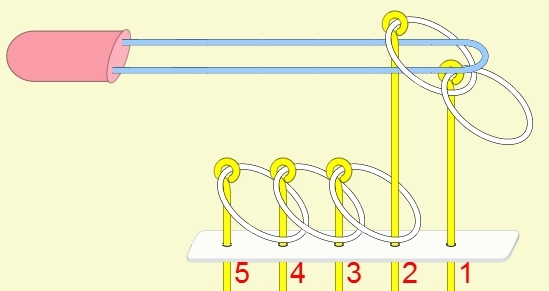
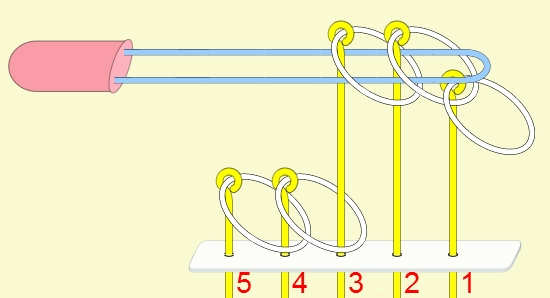
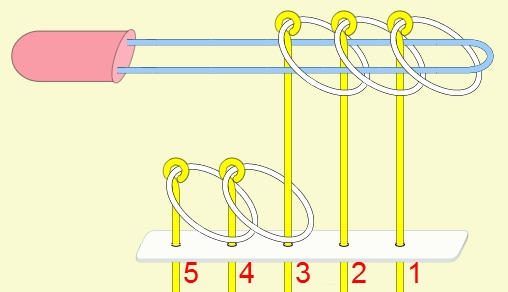
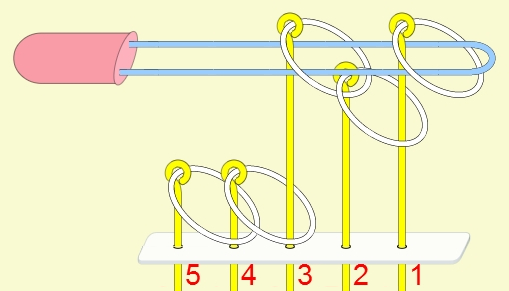
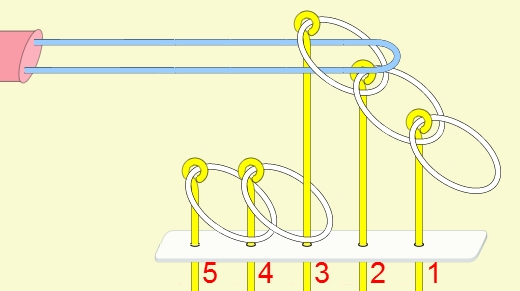
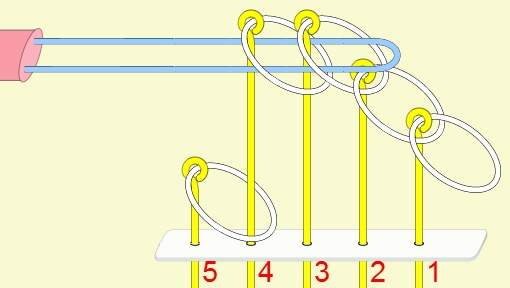
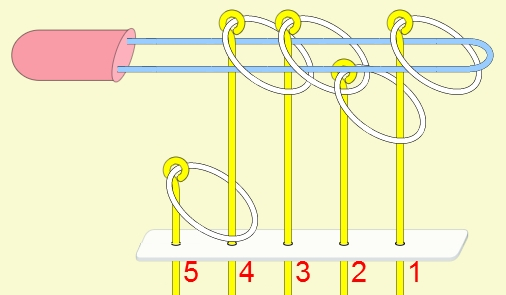
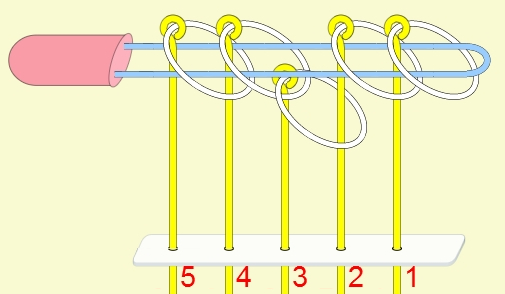
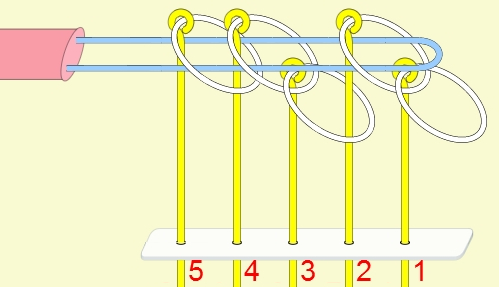
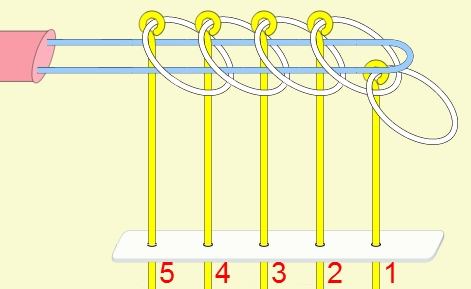
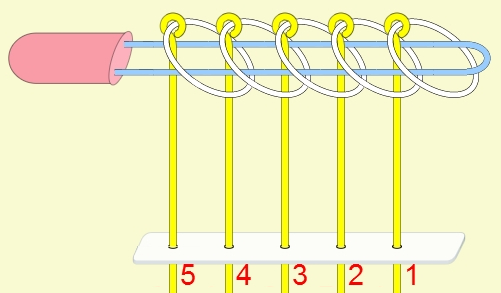
        九連環的每個環是互相牽制的，除了第１環，要上下其他環是要在特定的狀態下才可以的，其規則有二：

      規則一：第１環可以在任何時候放上或取下。

      規則二：想放上或取下第Ｎ環 (N > 1)，就必須：
　        　         將第 N-1 環放在柄上，而第 1 到 N-2 環全部取下，如此才能放上或取下第 N 環。

        例：取下第9環

1-7 環全部在柄下，第8環在柄上，此時第9環可以放上或取下。

九連環與遞迴

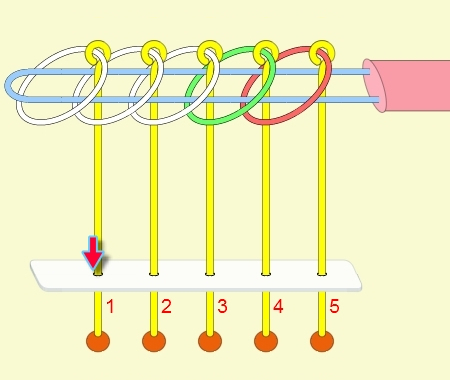
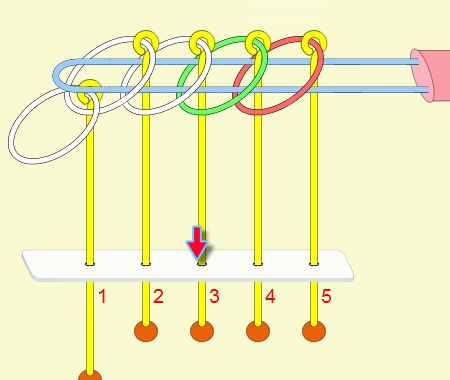
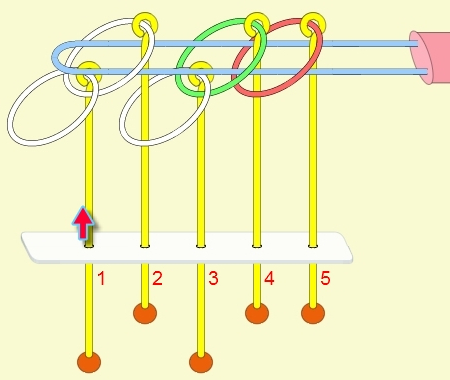
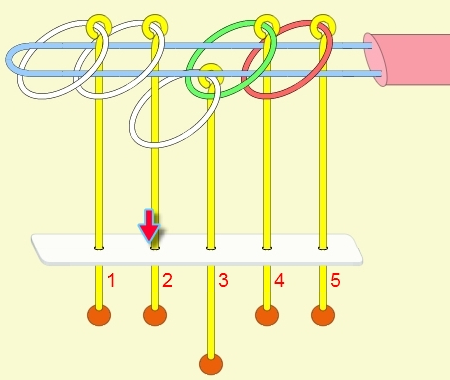
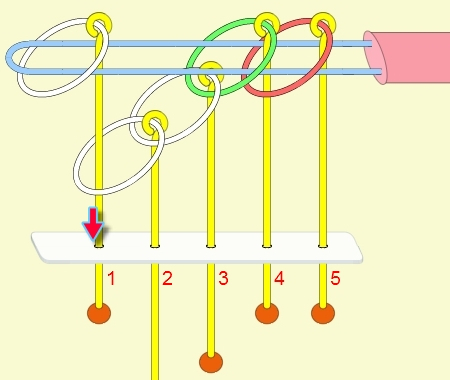
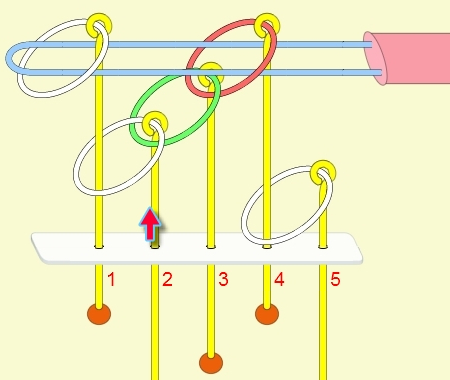
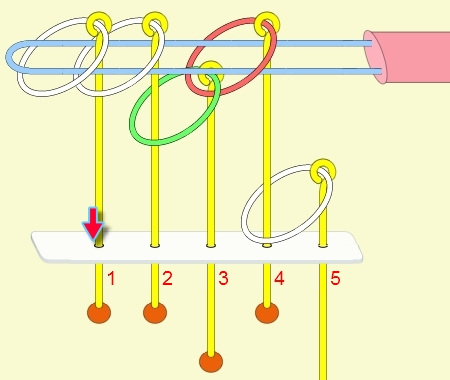
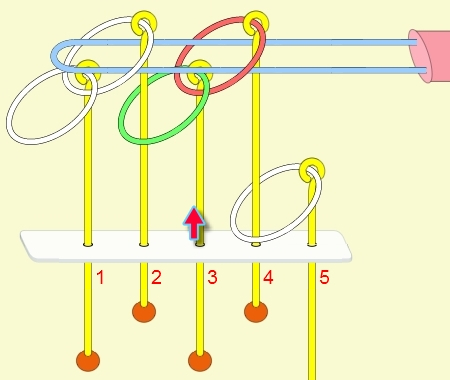
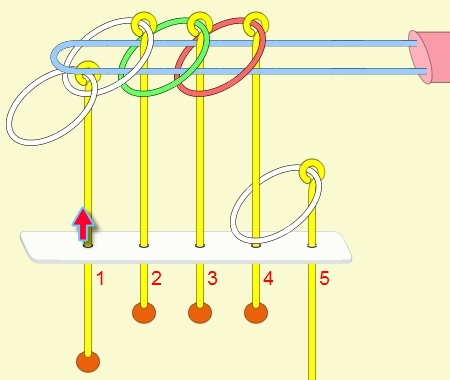
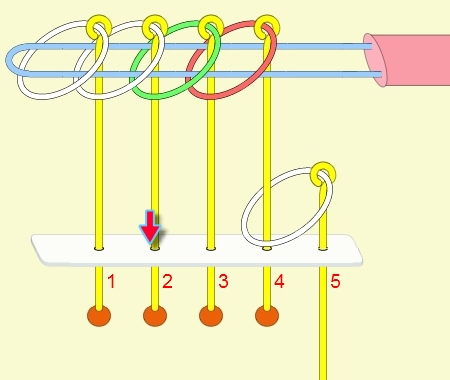
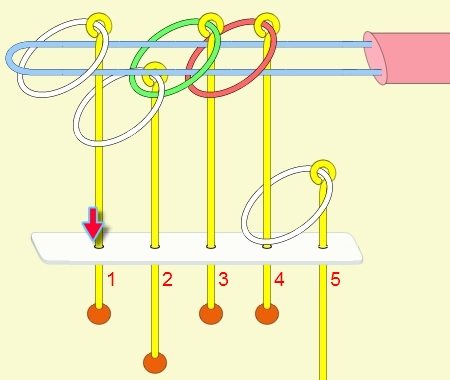
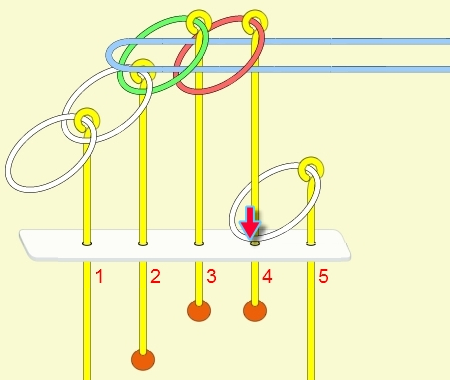
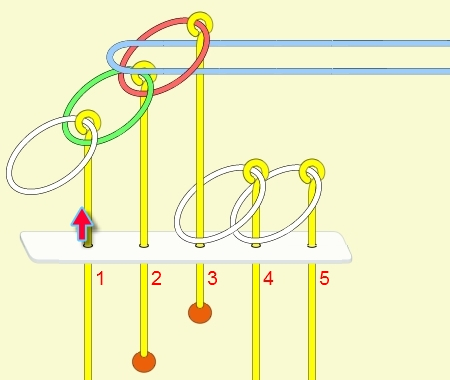
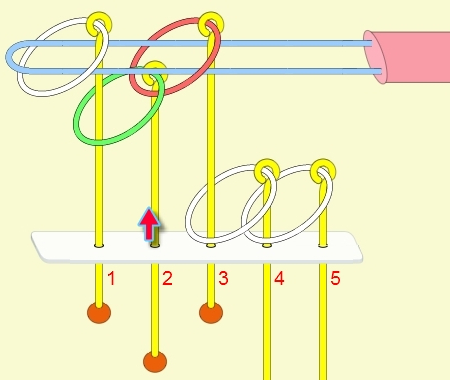
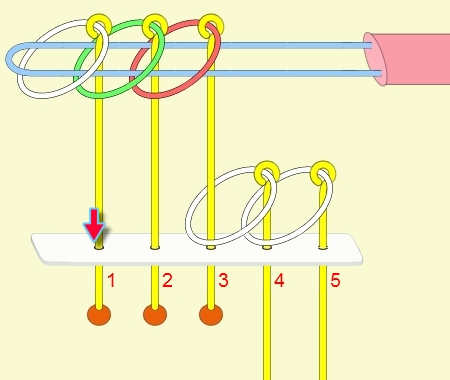
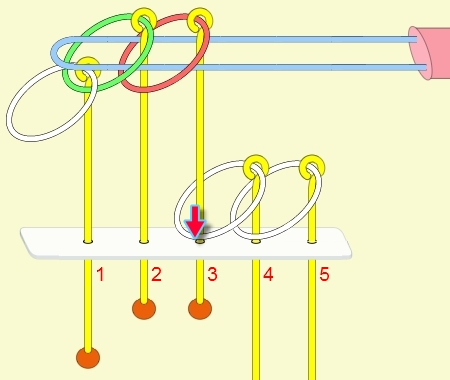
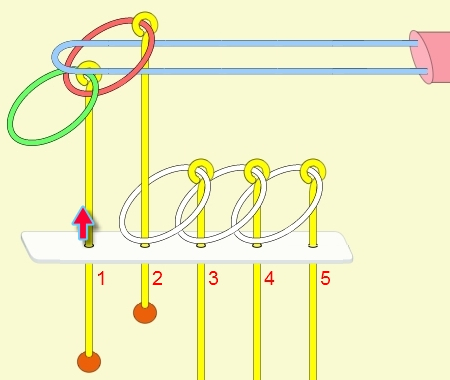
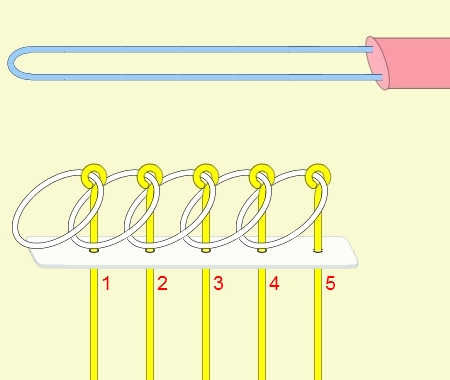
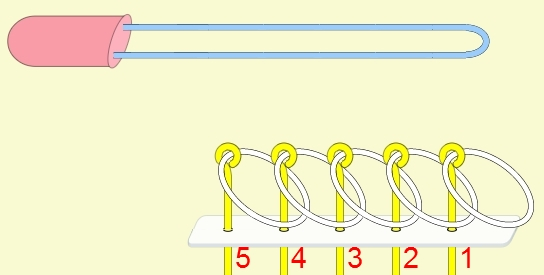
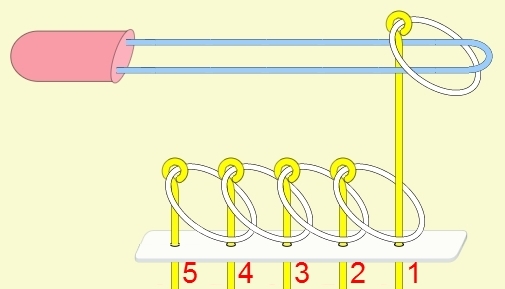
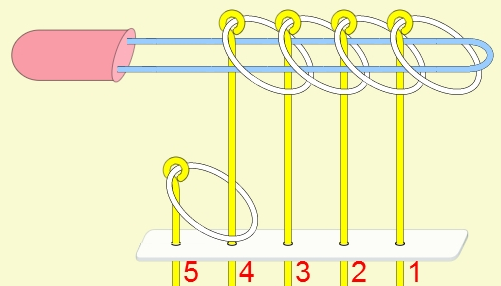
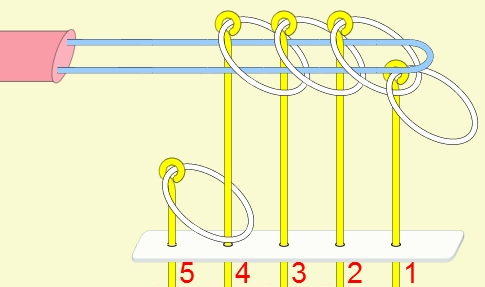
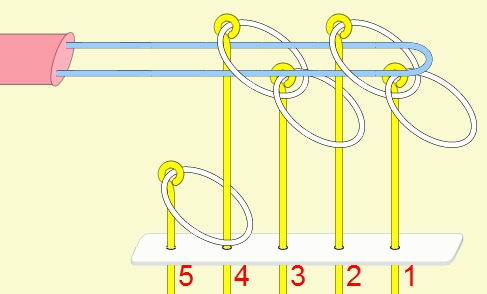
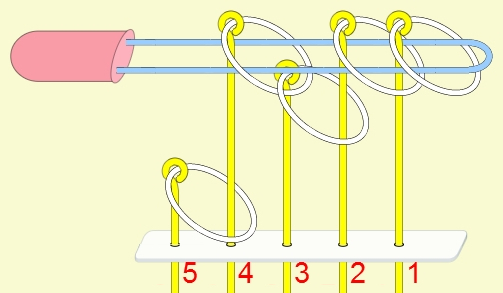
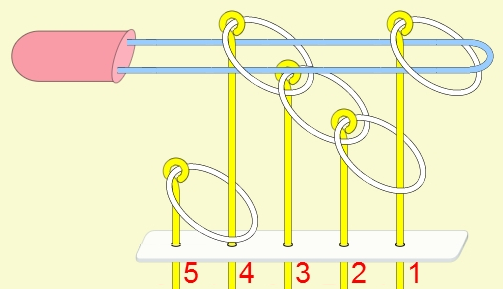
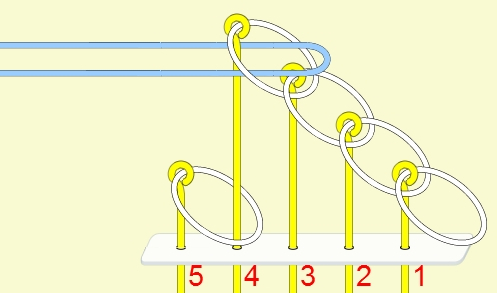
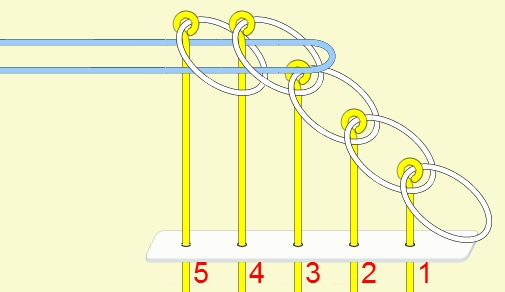
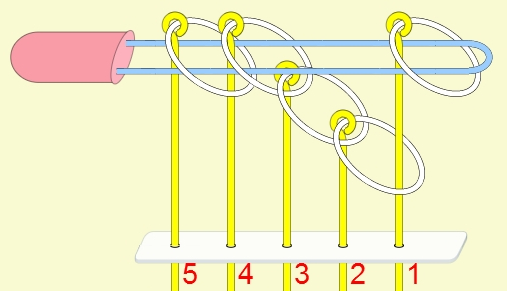
        九連環的拆解過程是一種遞迴式，關於遞迴程式可參考疊代與遞迴這篇文章，其內文所介紹的範例均為直接遞迴，
        而九連環會用到直接遞迴與間接遞迴，感覺好像很複雜，其實遞迴是相當直覺的，由例子直接說明。

        以5連環全解來說明，目的是要將5個環全部取下:

(00)	(01)
同遞迴的思考方式由外而內推導: 即由最後一環往前推導，思考如何把第5環取下，要把第5環取下，依規則先要取下1到3環，才能取下第5環而要下第3環必須第1環在下，第2環在上，所以要先下第1環 (目的：第5環要下）	此時可下第3環 (目的：第5環要下）
(02)	(03)
下第2環必須第1環在上，所以要上第1 環 (目的：第5環要下）	此時可下第2環 (目的：第5環要下）
(04)	(05)
下第1環 (目的：第5環要下）	終於可以下第5環了步驟01到05可以看成是3個環全下的方式即要下第N個環，要先下1到(N-2)個環
(06)	(07)
這時要下第4環，必須第3環在上，第3環要上則必須第2環在上，第2環要上則必須第1環在上，所以先上第1環 (目的：第4環要下）	第2環上 (目的：第4環要下）
(08)	(09)
第3環要上，必須第1環下 (目的：第4環要下）	此時可上第3環 (目的：第4環要下）
(10)	(11)
第2環要下，所以第1環要上 (目的：第4環要下）	第2環下 (目的：第4環要下）有沒有發現，步驟07到11，相當於把1到3個環全上的方式而目前狀態可看成4個環全下的狀態這是一個遞迴的狀態，相當於下完第5環後，再把1到3環全上，然後變成4個環全下的遞迴
(12)	(13)
第1環下 (目的：第4環要下）	可以下第4環了
(14)	(15)
要下第3環必須第2環上，第2環要上，必須第1環上 (目的：第3環要下）	第2環上 (目的：第3環要下）
(16)	(17)
第1環下 (目的：第3環要下） 3環全下的遞迴狀態	可以下第3環了
(18)	(19)
第2環要下，必須第1環要上 (目的：第2環要下）	第2環下 (目的：第2環要下） 2環全下的遞迴狀態
(20)	(21)
第1環下 (目的：第1環要下）	完成

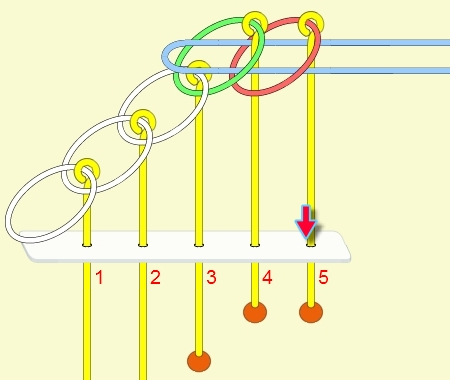
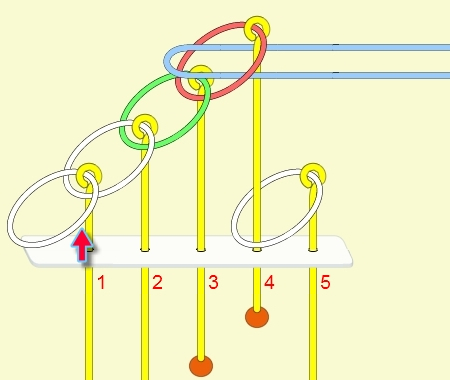
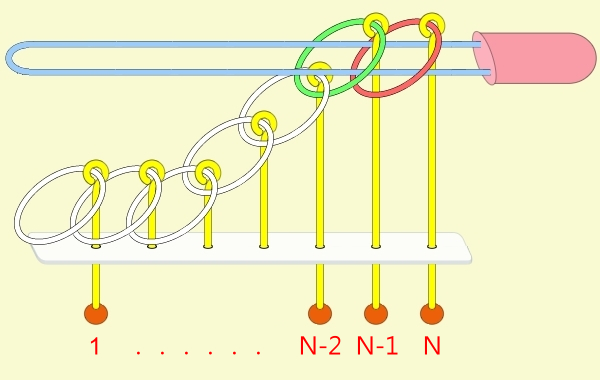
   遞迴解說:

       由上面的例子可看出:
       (1) 步驟01到05，相當於3個環全下的方式。
       (2) 步驟06為，放下第5環。
       (3) 步驟07到11，相當於3個環全上的方式。
       (4) 步驟12開始，變成 4個環全下的遞迴。

   推廣到 N 連環全下，其遞迴步驟為:

	(1)
	1至N-2個環全下
	(2)
	取下第N環
	(3)
	1至N-2個環全上此時為 N-1連環全下的遞迴狀態
	(4)
	1至N-1個環全下

推廣到 N 連環全上，其遞迴步驟為:

	(1)
	1至N-1個環全上
	(2)
	1至N-2個環全下
	(3)
	放上第N環此時為 N-2連環全上的遞迴狀態
	(4)
	1至N-2個環全上

遞迴式:

allRingDown(N) = allRingDown(N-2) + showRingDown(N) + allRingUp(N-2) + allRingDown(N-1)

allRingUp(N) = allRingUp(N-1) + allRingDown(N-2) + showRingUp(N) + allRingUp(N-2)

        allRingDown(N) : 第 1 ~ N 環全下；allRingUp(N) : 第 1 ~ N 環全上

        showRingDown(N) : 顯示第N環下的動作；showRingUp(N) : 顯示第N環上的動作

        其中 allRingDown(N)為遞迴函式 :
        (1) 直接遞迴 : 呼叫 allRingDown(N-2) 及 allRingDown(N-1)
        (2) 間接遞迴 : 呼叫 allRingUp(N-2)

        其中 allRingUp(N) 為遞迴函式:
        (1) 直接遞迴 : 呼叫 allRingUp(N-1) 及 allRingUp(N-2)
        (2) 間接遞迴 : 呼叫 allRingDown(N-2)

    九連環遞迴程式碼:

JavaScript:

程式可於 jsBin 線上執行.

另外為 C 語言所寫的 Windows console program: nineLinkedRings.zip

九連環與格雷碼

       由於遞迴式不太適合用來寫九連環遊戲，一般若無適當的疊代法(iteration)就只能用推疊(stack)取代遞迴呼叫，
       經網路搜尋後找到了格雷碼。另人驚訝的是格雷碼的順序居然完全和九連環解法的順序相同。

      先看看什麼是格雷碼：

        格雷碼 (Gray Code)是由貝爾實驗室的Frank Gray在1940年代提出的，用來在使用PCM（Pusle Code Modulation）
        方法傳送訊號時避免出錯。格雷碼是一個數列集合，相鄰兩數間只有一個位元改變，為無權數碼。(參6)

        數字0～7的編碼比較如下：

十進位	格雷碼	二進位
0	000	000
1	001	001
2	011	010
3	010	011
4	110	100
5	111	101
6	101	110
7	100	111

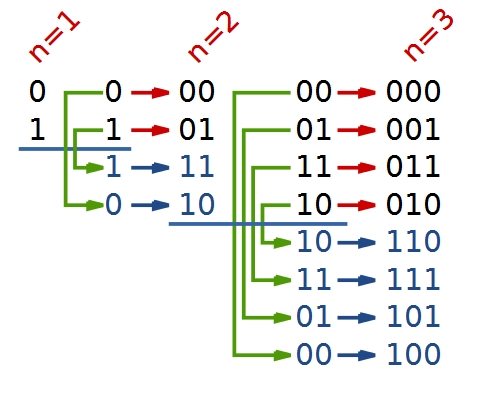
格雷碼的鏡射排列:

n位元的格雷碼可以從n-1位元的格雷碼以上下鏡射後加上新位元的方式快速的得到，如下圖所示。(參6)

九連環與格雷碼的關係:

步數	5連環全部放上的順序	格雷碼	二進制
00		00000	00000
01		00001	00001
02		00011	00010
03		00010	00011
04		00110	00100
05		00111	00101
06		00101	00110
07		00100	00111
08		01100	01000
09		01101	01001
10		01111	01010
11		01110	01011
12		01010	01100
13		01011	01101
14		01001	01110
15		01000	01111
16		11000	10000
17		11001	10001
18		11011	10010
19		11010	10011
20		11110	10100
21		11111	10101

        由上圖可以看出，解九連環的順序就是格雷碼的順序，不禁讓人懷疑，法蘭克．格雷(Frank Gray)是不是有玩過九連環？

    格雷碼與二進制的轉換：

        由於格雷碼為無權數碼，無法直接拿來運算，但可以經由與二進制的互換，得到格雷碼的值與順序的關係。
        轉換方法如下或參考 Converting Between Gray and Binary Codes 中非常清楚的動態說明。

       二進制碼轉換成格雷碼:(參7, 參8)

    g(1) = b(1)
    g(2) = b(1) xor b(2)
    g(3) = b(2) xor b(3)
    g(4) = b(3) xor b(4)
    g(5) = b(4) xor b(5)

JavaScript:

    function binaryToGray(num)
    {
        return (num >> 1) ^ num;
    }

格雷碼轉換成二進制:(參7, 參8)

   b(1) = g(1)
   b(2) = b(1) xor g(2)
   b(3) = b(2) xor g(3)
   b(4) = b(3) xor g(4)
   b(5) = b(4) xor g(5)

JavaScript:

    function grayToBinary(num, numBits)
    {
        var shift;
        for(shift = 1; shift <numBits; shift=2*shift) {
            num = num ^ (num >>shift);
        }
        return num;
    }

九連環遊戲

        九連環的遊戲是用 JavaScript 寫成，其中連環的動態動作是以 KineticJS javascript framework 完成。

        由於九連環的狀態與順序的關係即為格雷碼與順序的關係，遊戲中所顯示的剩餘步數(左下)，提示，自動，
        均是由九連環的狀態對應到格雷碼，然後由格雷碼轉成二進制，並作加減法運算，再轉回格雷碼而來的。

程式原始碼

        GitHub: https://github.com/SimonHung/NineLinkedRings
        Simon's GitHub Projects: https://simonhung.github.io

參考資料

        (1) 純手工打造-迷你九連環: http://whereyou.pixnet.net/blog/post/22696509
        (2) 九連環拆裝攻略: http://game.titan24.com/tbm/news/2009-09-10/133.html
        (3) 直立式九連環: http://www.wzweiao.com/1338.htm
      (4) 成人益智玩具: http://www.chinastuffedtoys.com/new_view.asp?id=4305
        (5) Spin Out 線上遊戲: http://www.puzzles.com/products/SpinOut/PlayOnline.htm
        (6) 格雷碼 wiki: http://zh.wikipedia.org/wiki/格雷碼
        (7) Gray Code from/to binary and decimal: http://www.matrixlab-examples.com/gray-code.html
        (8) Gray code wiki: http://en.wikipedia.org/wiki/Gray_code

01/15/2013

如有版權問題，請告知。