Backtracking 回溯

(Backtracking)

Backtracking is a general algorithm for finding all (or some) solutions to some computational problem, that incrementally builds candidates to the solutions, and abandons each partial candidate c ("backtracks") as soon as it determines that c cannot possibly be completed to a valid solution.(參1)

回溯法是一種用來找尋問題所有解(或部份解答)的通用演算法(general algorithm)；當問題的解答是由一系列的選擇所組成時，運用遞迴遞增地建立所有可能的組合方案，並於建立過程中去除不可能的組合，最終得到所要的答案。

範例: 字串全排列

        思考方式:這跟思考計算如何由 M取 N個數來排列一樣，以 A, B, C 全排列( 3取 3排列)說明:
        假設有 3個位置來放置 A,B,C，第1個位置由 3個取任意1個有3種取法，第2個位置由剩餘的2個取任意1個有2種取法，
        最後1個位置只剩1種可取，所以排列數為： 3X2X1 = 6 (3!)

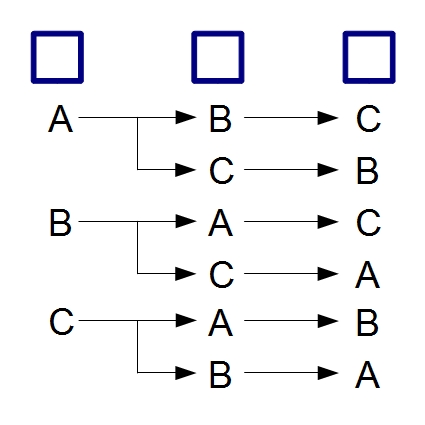
其程式解法亦相同，由未選取的依序取一數排在第1位，再由剩餘的依序取一數排第2位，如此遞迴直到全部取完，
再回溯到前一位置並由上一個順序往下取未選取的，再遞迴至下一位置，取剩餘的，如此循環直到所有順序都取完，即為全排列。

JavaScript

//----------------------------------------------------------------------------------------------
// Permutation 排列
//
// reference: Lecture 10 | Programming Abstractions (參2.1)
//
// soFar: 目前已選取, rest: 剩餘可選擇，當沒有剩餘就印出並回溯。
//----------------------------------------------------------------------------------------------
function recPermute(soFar, rest)
{
        if(rest === "") { //沒有可選擇了
                document.write("<div>" + soFar +"</div>"); //印出結果, 並回溯
        } else {
                //還有可選擇
                for(var i = 0; i < rest.length; i++) { //由所有可選擇中依序取一

                        var next = soFar + rest.charAt(i); //由可選擇取一,與目前所選擇組合(串接)

                        var remaining = rest.substr(0,i) + rest.substr(i+1); //移去已取出的 rest[i]

                        recPermute(next, remaining); //由剩餘的來取出下個位置的字元(遞迴建立所有可能的組合)　
                }
        }
}

function listPermutation(listString)
{
        recPermute("", listString);
}

listPermutation("ABC");

程式可於 jsBin online 執行.

執行過程: (參2.2)

範例: 3個分數相加等於1，說明如下: (參3)

下圖3個分數的分母為2位數，分子為1位數，分別由未知數 a,b,c,d,e,f,g,h,i 表示，求 a/bc + d/ef + g/hi = 1, 時的解,
a~i 為1~9其中的一個數字, 且數字不得重複。

思考方式:這個題目的解法可以看成是上一題程式的應用，除了全排列是將所有的可能全部列出外，回溯法就是由全部
的可能中去除不可的的方案即為所要的答案，所以這一題只要由上一題再加列印出可能的解答即可。

JavaScript

//=================================================================================
//
// Three Fractions
//
// a/bc + d/ef + g/hi = 1
//
// Each of three fractions has a one-digit numerator and a two-digit denominator.
// The three fractions together add up to one.
// Place the nine digits 1-9 into the fractions to make the equation correct.
//
// Source: Nob Yoshigahara, c/o Scot Morris in OMNI, April 1994. Used as Ken's POTD 4/14/94.
//
// URL: http://ken.duisenberg.com/potw/archive/arch97/970111sol.html
//=================================================================================

function printSolution(n)
{
        var denominator1 = parseInt(n[1]) * 10 + parseInt(n[2]); //分母
        var denominator2 = parseInt(n[4]) * 10 + parseInt(n[5]);
        var denominator3 = parseInt(n[7]) * 10 + parseInt(n[8]);
        var commonDenominator = denominator1 * denominator2 * denominator3; //通分(公分母)

        var totalNumerator = parseInt(n[0]) * denominator2 * denominator3 + //分子通分相加
                                            parseInt(n[3]) * denominator1 * denominator3 +
                                            parseInt(n[6]) * denominator1 * denominator2;

        if(totalNumerator == commonDenominator) { // 分子等於分母, 即和等於 1
                document.write("<div>" +
                                            n[0] + "/" + n[1] + n[2] + " + " +
                                            n[3] + "/" + n[4] + n[5] + " + " +
n[6] + "/" + n[7] + n[8] + " = 1 " +
                "</div>");
        }
}

function recPermute(soFar, rest)
{
        if(rest === "") {
                printSolution(soFar); //印出符合條件的解答
        } else {
                for(var i = 0; i < rest.length; i++) {

                        var next = soFar + rest.charAt(i);

                        var remaining = rest.substr(0,i) + rest.substr(i+1);

                        recPermute(next, remaining);
                }
        }
}

function solution()
{
        recPermute("", "123456789");
}

solution();

程式可於 jsBin online 執行.

回溯法屬於暴力法(Brute-force)的一種，若將問題的所有可能解答，表示成一個稱為狀態空間樹(State Space Tree)的樹狀結構，其解法就類似 "深度優先搜尋法"(DFS)。(參4)

關於用回溯法解問題的題目有很多，如：數獨(Sudoku), 著色問題...等，也許有機會再補充。

參考資料

        (1) Backtracking wiki: http://en.wikipedia.org/wiki/Backtracking
        (2) Lecture 10 | Programming Abstractions (Stanford) YouTube: http://youtu.be/NdF1QDTRkck
        (3) 這個題目是多年前同學寄給我的: http://ken.duisenberg.com/potw/archive/arch97/970111sol.html
              經網路找尋結果可能是 Nob Yoshigahara 的作品 (puzzle 設計大師，之後應該會看到他的作品)
        (4) 回溯、分枝與限制 : http://sjchen.im.nuu.edu.tw/Algorithm/97Spring/Course08.pdf

如有版權問題，請告知。